Water is the elixir of life, water gives life and water IS life. Phrases like these are well known in the vernacular. What is behind these statements? And what do water and mobile communications have to do with each other? We know that without water there would be no life on this planet. Water is more than a thirst quencher or a detergent: it provides energy for life processes, in fact, in our bodies water works like a battery1)Pollack, G.H. : The fourth phase of water. Beyond solid, liquid and vapor. Ebner and Sons Publishers, 2013!
In order to understand this fact, research on the water element must be included and we must reflect on the vitality of waters. Vital, living waters are in motion, they must flow naturally and be able to swirl around their own axis in a spiral. If you force waters into an unnatural straight course, they lose their natural balance and have a destructive effect. This was recognised by the naturalist and forester Viktor Schauberger in the first half of the 20th century2)Schauberger, J. (2009): Viktor Schauberger. Das Wesen des Wassers. Original texts, edited and commented by Jörg Schauberger. AT Verlag, 3rd edition, 2009.
Polarity creates a dynamic balance
 The meanders of a free-flowing river, the swinging back and forth of the river, illustrate the principle of polarity that characterises our world. It is polarity – the presence of two opposite poles – that gives strength to life and creates vitality. It was Johann Wolfgang Goethe who recognised polarity as one of nature’s two great driving forces and described how it powers processes in the material through “attraction and repulsion”, while the progression, the “ever-evolving ascent” as the second driving force in the sense of Goethe promotes the development in the spiritual3)Goethe, J.W. (1828): Explanations on the aphoristic essay “Die Natur”, Weimar, 1828.
The meanders of a free-flowing river, the swinging back and forth of the river, illustrate the principle of polarity that characterises our world. It is polarity – the presence of two opposite poles – that gives strength to life and creates vitality. It was Johann Wolfgang Goethe who recognised polarity as one of nature’s two great driving forces and described how it powers processes in the material through “attraction and repulsion”, while the progression, the “ever-evolving ascent” as the second driving force in the sense of Goethe promotes the development in the spiritual3)Goethe, J.W. (1828): Explanations on the aphoristic essay “Die Natur”, Weimar, 1828.
Yin-Yang, male-female, movement-calm, cold-heat: The two poles complement each other and together create a dynamic balance. Not surprisingly, the greatest diversity in nature occurs where opposites meet4)Gastl, M. (2015): Drei-Zonen-Garten: Vielfalt · Schönheit · Nutzen, Publisher Dr. Friedrich Pfeil. In dry poor meadows, for example, which are located next to a wet, shady zone on the edge of a water, biodiversity is abundant.
Polarity in chemistry refers to the formation of separate charge centers; in this way, both negative and positively charged areas can exist in polar substances. Between positively and negatively charged poles, an electrical potential arises: it is the voltage between the two poles that generates the energy in a battery5) The World Foundation for Natural Science (2021): All life works electrically. Video and articles, https://www.naturalscience.org/news/2021/04/all-life-works-electrically/.

Although it is outwardly and as a closed body of water electrically neutral, water contains this life-giving polarity in two respects: both in the water molecule H2O as well as in the body of water (for example, water in a glass, in natural waters, and in our body water) charge separations are present. There are areas with excess electrons and a negative charge, and areas with an electron deficiency and a positive charge.
From the textbooks the knowledge of water as a polar compound is known, it is called a dipole, because its electron density is distributed asymmetrically within the H2O molecule6)https://www.chemie.de/lexikon/Polarit%C3%A4t_%28Chemie%29.html. As a dipole, the water molecule has two differently charged electric poles: a negative charge on the side of the oxygen atom, a positive charge on the side of the two hydrogen atoms. The water molecule can therefore be compared with a bar magnet. Electromagnetic waves, especially microwave radiation (the frequency range used for mobile communications) bring this “bar magnet”, i.e. the water dipole, into rotation. This is because if such an electromagnetic wave runs over the dipole, its minus pole, respectively its plus pole, are constantly reorienting themselves according to the electromagnetic wave. This principle is also used with the microwave oven: through the rotation of the water molecules they begin to vibrate in such a way that they rub against each other, which generates heat – the food is heated. This is then referred to as the thermal effect of microwave radiation.
Microwave radiation: not only thermal but also biological effects
But the convenience of the microwave oven comes at a price: as early as 1992, Dr. Hansueli Hertel was able to prove that the blood levels of test persons changed significantly when they ate foods prepared in the microwave oven. For example, after eating microwave irradiated food, the haematocrit level was greatly increased7)Blanc, B. H. / Hertel, H. U. (1992): ComparativesStudy about the influence on man by food prepared conventionally and in the microwave oven. 8)The World Foundation for Natural Science (2002): Cooking with microwaves? The Kiss of Death!! …. or, rather, a guaranteed recipe for cancer!! The Journal of Natural Science, 2nd extended edition, 2002. The haematocrit level describes the proportion of blood cells in the total of blood and thus the fluidity of the blood. If the fluid content of the blood decreases, the haematocrit increases.
A high haematocrit level therefore means that the blood is more viscous and flows more slowly, increasing the risk of thrombosis or stroke, for example. However, as Dr. Hertel’s research shows, haematocrit levels had decreased after eating raw food or conventionally cooked food. Dr. Hertel’s research causes us to sit up and take notice: microwave radiation changes more than just the temperature of a medium. Many studies have already shown biological effects that occur independently of tissue warming9)Bioinitiative (2020): Reported Biological Effects from Radiofrequency Radiation at Low-Intensity Exposure, https://bioinitiative.org/updated-research-summaries/, Download 04/2021.
Our own research10)Ulrich, D. (2020): Impact of mobile communications on water and life. Study situation and own experiments, 2020shows other evidence: water is not only heated in the microwave oven, but it also changes its order11)See also in Warnke, U. (2019): Bionisches Wasser. Das Supermolekül für unsere Gesundheit, arkana. This can be made visible by means of dark field microscopy. After drying a drop of water, the dark field filter in the microscope makes the structures of the deposited sediments, the salts dissolved in the water and other substances visible. Each water thus leaves its own pattern. In a test, the reference water, a Swiss mineral water from the supermarket, was brought to the boil, dripped on after cooling and dried. The structure of the water boiled with gas is similar to that of the original water: a blue center, a star-shaped pattern around the center and semi-concentric circles. After cooking in the microwave oven, not much can be seen of the original sediment pattern, it is destroyed.

How does this loss of order come about? In search of an explanation, it is worth taking a look at water research. Several scientists have found that water molecules can arrange in different ways when merging into so-called water clusters (i.e. groups of H2O molecules), the water shapes into different structures12)For example in: Engler, I. (2009): Wasser. Polaritätsphänomen, Informationsträger, Lebens-Heilmittel; Pollak, G.H. (2013): The fourth phase of water. Beyond solid, liquid, and vapor; Wiggins, P. (2008): Life Depends upon Two Kinds of Water. PLoS ONE 3(1): e1406. doi:10.1371/journal.phone.0001406; Jhon, M. S. & Pangman, MJ (2012): Hexagonales Wasser: Der Schlüssel zur Gesundheit, Mobiwell Verlag, 2nd edition. Original edition: Jhon, M. S.: The Water Puzzle and the Hexagonal Key, And: Hexagonal Water, The Ultimate Solution; Ho, M.-W. The rainbow and the worm (2008). The physics of organisms. World Scientific.; Cowan, T. (2019): Cancer and the new Biology of Water.. The water structure changes depending on factors such as temperature, surface condition of adjacent materials or vortex. Changes on the cluster level affect the flow property of waters. Viktor Schauberger had described this with the towing properties of mountain streams when transporting tree trunks13)Schauberger, J. (2009): Viktor Schauberger. Das Wesen des Wassers. Original texts, edited and commented by Jörg Schauberger. AT Verlag, 3rd edition, 2009. The same thing happens in the drop under the microscope: Depending on the water structures, the flow property in the drop changes during the drying process. Thus, each water has its own deposition pattern. The patterns indicate the energy inherent in the water.
Water structures: EZ water and bulk water
Today, at least two different types of water structure are known. One of these structures is water in the conventional sense, which shows a more or less random network of water molecules, which, through hydrogen bridges are connected quite loosely to fragmentary chains14)Clegg, J.S. (1984): lntracellular Water and the Cytomatrix: Some Methods of Study and Current Views, The Journal of Cell Biology, Vol. 99, No. 1, Part 2, 1984. In literature, this water is often called bulk water.
In contrast to the bulk water there is highly structured water. Here, the molecules arrange themselves into hexagons; due to its structure, this water is very close to the ice. Professor Gerald Pollack15)https://www.pollacklab.org/ of the University of Washington in Seattle is currently the leading scientist when it comes to studying hexagonal water. He coined the term “EZ water” for this highly structured, liquid-crystalline water. EZ stands for “Exclusion Zone”, because in this zone in the water, other substances are excluded, it consists only of hydrogen and oxygen. In the EZ, an alkaline pH value and a negative electrical charge are measured. Due to the crystal-like arrangement of the molecules, the water is more viscous than other water, it is a gel.
Biologist James Clegg studied cell water in the 1990s and discovered that in addition to bulk water, gel-like water with a higher degree of order is also present in a cell, and its formation depends heavily on the interfaces present in the cell structures, such as cell skeletons, polymers, or enzymes.16)Glegg, J.S. (1981;1984), in: Bischof, M. (2002): Biophotonen. Das Licht in unseren Zellen, Verlag Zweitausendeins, 12th edition, 2002
For our bodies, plants, and many natural systems, the coexistence of differently structured waters is vital. The reason for this: while EZ water is negatively charged, bulk water has a positive charge. The charge differences generate voltage and thus valuable energy, which is used for life processes. The presence of various waters drives life, as the doctor Ivan Engler states17)Engler, I. (2009): Wasser. Polaritätsphänomen, Informationsträger, Lebens-Heilmittel. Spurbuchverlag, 2009.
If the structuring of water is so important for life, but we know from research that microwave radiation is harmful to life18)The World Foundation for Natural Science (2021): Animals and plants under radiation stress. Video and articles. https://www.naturalscience.org/news/2021/02/animals-and-plants-under-radiation-stress/, an important question arises: Does microwave radiation have an influence on the water structure?
Based on the findings on the vitality of waters provided by research with dark field microscopy, it makes sense to approach this question with the same method. Does the deposition pattern change in water samples exposed to Wi-Fi radiation from Wi-Fi routers and smartphones?

The picture above shows a drop of the original water as reference water. There is a large amount of blue, which according to G. H. Pollack indicates the presence of EZ19)Pollack, G.H. (2014): The fourth phase of water. Beyond solid, liquid and vapor. Ebner and Sons Publishers, 2013. In addition, a great order can be detected, with a small center, concentric circles, and meander-like flow structures towards the edge. After being exposed to a Wi-Fi router and a smartphone for 30 minutes, a completely different picture emerges. Black areas are areas without sediments. Evidently, the water has lost its tractive force, the sediments were mostly deposited at the edge of the drop.
Further samples show a similar picture. The lack of tractive force is very noticeable in the next example: On the left the control water with many blue components and ordered, concentric, albeit very rigid rings.

After Wi-Fi irradiation, the large, sediment-free center and the absence of the original pattern stand out. We remember the destroyed pattern of the water boiled in the microwave oven: The same frequency is used for Wi-Fi as with the microwave oven: 2.45 GHz! This is crucial, because 2.45 GHz is an important frequency for water since it absorbs maximum energy from this spectral range. 2.45 GHz is therefore a typical water frequency, as are other frequencies in the microwave spectrum used in mobile communications.
Water can react differently to Wi-Fi radiation. The extent of the influence of radiation on the flow property also depends on the characteristics of the original water. However, the disturbed tractive force tends to always be present, as another three water samples show in the picture below.
But what exactly does Wi-Fi irradiation “do” with the water structures and the voltage they generate? In fact, preliminary results from water structure research suggest that water exposed to Wi-Fi radiation reduces the EZ zone by about 15 percent20)Cowan, T. & Fallon Morell, S. (2020): The Contagion Myth, Skyhorse Publishing, 2020. This finding raises further questions:
- Does the reduction of EZ water by Wi-Fi also occur with mobile communications in other frequencies and pulsations?
- Does water no longer provide energy when the zone with structured water is reduced?
- What does the resulting lack of energy mean for cell processes, for organs, for us humans, animals, and plants?
There is clear evidence that the change in water structures caused by mobile communications disrupts and endangers life processes. It has been shown in experiments that EZ water is involved in capillary action, for example21)Pollack, G.H. (2017): Lecture at the Three-Country Congress, Konstanz, 15.10.2017. It is well documented that trees exposed to microwave radiation are under stress, and the tips of their leaves turn brown and are eventually shed22)The World Foundation for Natural Science (2021): Animals and plants under radiation stress. Video and articles. https://www.naturalscience.org/news/2021/02/animals-and-plants-under-radiation-stress/. Whether this reaction is caused by an impairment of the capillary effect due to altered water structures is another open research question that should definitely be investigated!
Microwave radiation changes the blood
But it is not only plants that are under stress from microwave radiation. Does Wi-Fi radiation also change our body water? Our bodies are about 70% water, 99% of all molecules in our body are water molecules. The fact that mobile communications are a risk to our health has been shown multiple times23) Martin L. Pall (2019): 5G: Great risk for EU, U.S. and International Health! Compelling Evidence for Eight Distinct Types of Great Harm Caused by Electromagnetic Field (EMF) Exposures and the Mechanism that Causes Them. But does Wi-Fi radiation also change our body water?
Blood is a body fluid that reacts quickly to radiation. In the dark field microscope, enlarged 1000fold, the red blood cells become clearly visible. In the following picture, the left image shows beautifully round, freely distributed, red blood cells. This is the normal, healthy state of the blood. But with Wi-Fi radiation, so-called money rolls form in the blood (right picture)! In this state, the oxygen stored in the dent of the red blood cell can only be released insufficiently to the tissue. Also, the flow speed of the blood is often worse24)Christmann, H. (2020): Blut gut, alles gut. Laborwerte richtig deuten, Dunkelfeldmikroskopie nutzen. Silberschnur Verlag.
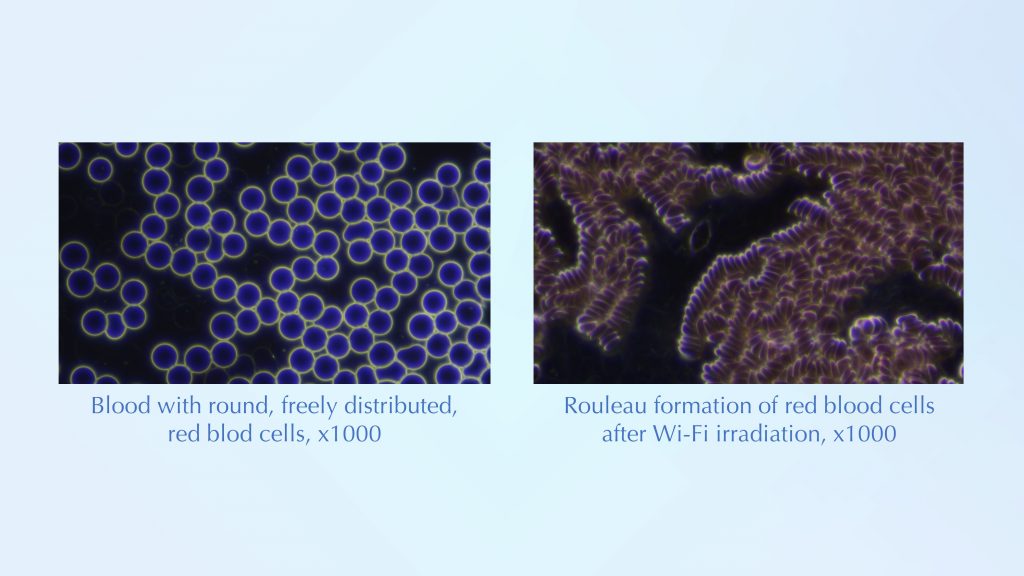
Biochemist Prof. Dr. Volker Ullrich confirms the money roll formation of the red blood cells. He cites as the cause the change of the voltage-dependent ion channel25)Ullrich, V. (2020): Neue Erklärungen für die Hypersensibilität aus der Neuro-Biochemie. oekoskop, Ärztinnen und Ärzte für Umwelschutz, Nr. 2/20, 2020. Ion channels are tube-shaped proteins that act like a door on the cell membrane and are permeable only to individual ion types. If the ion channels are voltage-controlled, they open at the membrane depending on the charge ratio. An example for this are the voltage-controlled calcium channels, which are influenced by mobile communications. Measurements show that the calcium level in the cells increases when exposed to mobile communications26)Martin L. Pall (2019): 5G: Great risk for EU, U.S. and International Health! Compelling Evidence for Eight Distinct Types of Great Harm Caused by Electromagnetic Field (EMF) Exposures and the Mechanism that Causes Them.. An increased concentration of calcium ions in the cells leads to increased cell death, oxidative stress, cardiac arrhythmias, neurological and neuropsychiatric consequences, and hormonal disorders27)The Epoch Times (2020): A summary of Martin Pall’s report can be found, for example, at https://www.epochtimes.de/wissen/us-professor-warnt-vor-5g-netz-gesundheitsrisiken-durch-verstaerkte-aktivierung-der-koerpereigenen-calciumkanaele-a3240322.html (16.5.2020) . Experiments showed that differently structured waters at the cell membrane co-control the function of the ion channels28)Wiggins, P. (2008) Life Depends upon Two Kinds of Water. PLoS ONE 3(1): e1406. doi:10.1371/journal.pone.0001406.This means that the ratio of highly structured water to bulk water at least co-determines the voltage at the cell membrane and thus the ion flow.
The current results indicate that microwave radiation interfere with the organisation of water. Also with the water in our bodies. It is obvious that this has an impact on our health. Children’s bodies have an even higher water content than the bodies of adults. Children therefore absorb the artificial microwaves more strongly, and health disorders and deformities occur more quickly.29)Trower, B. (2021): From zygote to foetus there is no hiding place from the electrically induced phase transition from 5G with its accompanying support and carrier waves. 2021-02=5G-No Hiding Place – Barrie Trower.pdf 30)Trower, B. (2019):The Danger of Microwave Technology, Fact Sheet The World Foundation for Natural Science. https://www.naturalscience.org/wp-content/uploads/2019/07/2019-10-16WFNSFSINTERVIEW-BARRIE-TROWERGEWEB.pdf
Water is an element that still holds many mysteries today, and recognising its essence and tasks is a prerequisite for the better understanding of life processes. In combination with the electromagnetic fields, the “blueprints” for life, water is at the beginning of life, because by restructuring its molecules, water has the ability to react to electromagnetic influences and to recreate electromagnetic fields.
Hormones, vitamins, nutrients, light, sound and – as the American doctor Thomas Cowan explains – even subtle energies such as feelings or thoughts can dock to the countless binding points of the crystal-like EZ water31)Cowan, T. (2018): Vaccines, autoimmunity and the changing nature of childhood illness, publisher: Chelsea Green Publishing. This water has the ability to interact with these influences and also change its shape depending on the input. One could therefore also claim that structured crystalline water forms a bridge between mind and matter. Biologist Mae-Wan Ho describes in her own words the property of water to react to the most subtle electromagnetic fields and to represent them in its structure. She considers body waters in organisms a kind of LCD, a liquid crystal screen that changes its structure depending on the electromagnetic pulse and thus shows a new image, a new structural composition32)Solution; Ho, M.-W. (2008): The rainbow and the worm. The physics of organisms. World Scientific..
If we put various artificial electromagnetic fields out into the world uncontrolled, as is currently happening with the further expansion of mobile networks, we interfere with the subtle organisation and communication in organisms, we play sorcerer’s apprentice. It is time to take seriously the many warnings given to us by nature, many scientists and our own bodies.
Let us, together, protect water and thus all life!
References
| ↑1 | Pollack, G.H. : The fourth phase of water. Beyond solid, liquid and vapor. Ebner and Sons Publishers, 2013 |
|---|---|
| ↑2, ↑13 | Schauberger, J. (2009): Viktor Schauberger. Das Wesen des Wassers. Original texts, edited and commented by Jörg Schauberger. AT Verlag, 3rd edition, 2009 |
| ↑3 | Goethe, J.W. (1828): Explanations on the aphoristic essay “Die Natur”, Weimar, 1828 |
| ↑4 | Gastl, M. (2015): Drei-Zonen-Garten: Vielfalt · Schönheit · Nutzen, Publisher Dr. Friedrich Pfeil |
| ↑5 | The World Foundation for Natural Science (2021): All life works electrically. Video and articles, https://www.naturalscience.org/news/2021/04/all-life-works-electrically/ |
| ↑6 | https://www.chemie.de/lexikon/Polarit%C3%A4t_%28Chemie%29.html |
| ↑7 | Blanc, B. H. / Hertel, H. U. (1992): ComparativesStudy about the influence on man by food prepared conventionally and in the microwave oven. |
| ↑8 | The World Foundation for Natural Science (2002): Cooking with microwaves? The Kiss of Death!! …. or, rather, a guaranteed recipe for cancer!! The Journal of Natural Science, 2nd extended edition, 2002 |
| ↑9 | Bioinitiative (2020): Reported Biological Effects from Radiofrequency Radiation at Low-Intensity Exposure, https://bioinitiative.org/updated-research-summaries/, Download 04/2021 |
| ↑10 | Ulrich, D. (2020): Impact of mobile communications on water and life. Study situation and own experiments, 2020 |
| ↑11 | See also in Warnke, U. (2019): Bionisches Wasser. Das Supermolekül für unsere Gesundheit, arkana |
| ↑12 | For example in: Engler, I. (2009): Wasser. Polaritätsphänomen, Informationsträger, Lebens-Heilmittel; Pollak, G.H. (2013): The fourth phase of water. Beyond solid, liquid, and vapor; Wiggins, P. (2008): Life Depends upon Two Kinds of Water. PLoS ONE 3(1): e1406. doi:10.1371/journal.phone.0001406; Jhon, M. S. & Pangman, MJ (2012): Hexagonales Wasser: Der Schlüssel zur Gesundheit, Mobiwell Verlag, 2nd edition. Original edition: Jhon, M. S.: The Water Puzzle and the Hexagonal Key, And: Hexagonal Water, The Ultimate Solution; Ho, M.-W. The rainbow and the worm (2008). The physics of organisms. World Scientific.; Cowan, T. (2019): Cancer and the new Biology of Water. |
| ↑14 | Clegg, J.S. (1984): lntracellular Water and the Cytomatrix: Some Methods of Study and Current Views, The Journal of Cell Biology, Vol. 99, No. 1, Part 2, 1984 |
| ↑15 | https://www.pollacklab.org/ |
| ↑16 | Glegg, J.S. (1981;1984), in: Bischof, M. (2002): Biophotonen. Das Licht in unseren Zellen, Verlag Zweitausendeins, 12th edition, 2002 |
| ↑17 | Engler, I. (2009): Wasser. Polaritätsphänomen, Informationsträger, Lebens-Heilmittel. Spurbuchverlag, 2009 |
| ↑18 | The World Foundation for Natural Science (2021): Animals and plants under radiation stress. Video and articles. https://www.naturalscience.org/news/2021/02/animals-and-plants-under-radiation-stress/ |
| ↑19 | Pollack, G.H. (2014): The fourth phase of water. Beyond solid, liquid and vapor. Ebner and Sons Publishers, 2013 |
| ↑20 | Cowan, T. & Fallon Morell, S. (2020): The Contagion Myth, Skyhorse Publishing, 2020 |
| ↑21 | Pollack, G.H. (2017): Lecture at the Three-Country Congress, Konstanz, 15.10.2017 |
| ↑22 | The World Foundation for Natural Science (2021): Animals and plants under radiation stress. Video and articles. https://www.naturalscience.org/news/2021/02/animals-and-plants-under-radiation-stress/ |
| ↑23 | Martin L. Pall (2019): 5G: Great risk for EU, U.S. and International Health! Compelling Evidence for Eight Distinct Types of Great Harm Caused by Electromagnetic Field (EMF) Exposures and the Mechanism that Causes Them |
| ↑24 | Christmann, H. (2020): Blut gut, alles gut. Laborwerte richtig deuten, Dunkelfeldmikroskopie nutzen. Silberschnur Verlag |
| ↑25 | Ullrich, V. (2020): Neue Erklärungen für die Hypersensibilität aus der Neuro-Biochemie. oekoskop, Ärztinnen und Ärzte für Umwelschutz, Nr. 2/20, 2020 |
| ↑26 | Martin L. Pall (2019): 5G: Great risk for EU, U.S. and International Health! Compelling Evidence for Eight Distinct Types of Great Harm Caused by Electromagnetic Field (EMF) Exposures and the Mechanism that Causes Them. |
| ↑27 | The Epoch Times (2020): A summary of Martin Pall’s report can be found, for example, at https://www.epochtimes.de/wissen/us-professor-warnt-vor-5g-netz-gesundheitsrisiken-durch-verstaerkte-aktivierung-der-koerpereigenen-calciumkanaele-a3240322.html (16.5.2020) |
| ↑28 | Wiggins, P. (2008) Life Depends upon Two Kinds of Water. PLoS ONE 3(1): e1406. doi:10.1371/journal.pone.0001406 |
| ↑29 | Trower, B. (2021): From zygote to foetus there is no hiding place from the electrically induced phase transition from 5G with its accompanying support and carrier waves. 2021-02=5G-No Hiding Place – Barrie Trower.pdf |
| ↑30 | Trower, B. (2019):The Danger of Microwave Technology, Fact Sheet The World Foundation for Natural Science. https://www.naturalscience.org/wp-content/uploads/2019/07/2019-10-16WFNSFSINTERVIEW-BARRIE-TROWERGEWEB.pdf |
| ↑31 | Cowan, T. (2018): Vaccines, autoimmunity and the changing nature of childhood illness, publisher: Chelsea Green Publishing |
| ↑32 | Solution; Ho, M.-W. (2008): The rainbow and the worm. The physics of organisms. World Scientific. |








